This explains the background to Euclidean rhythms really well:
15 Likes
Interesting read. It got me thinking about something about something that occurred to me a few months back. One thing that I donât think the author mentioned is that there are alternate ways (apart from the Euclid/Bjorkland approach) that can generate the same set of necklaces, in particular the Bressenham line drawing algorithm.
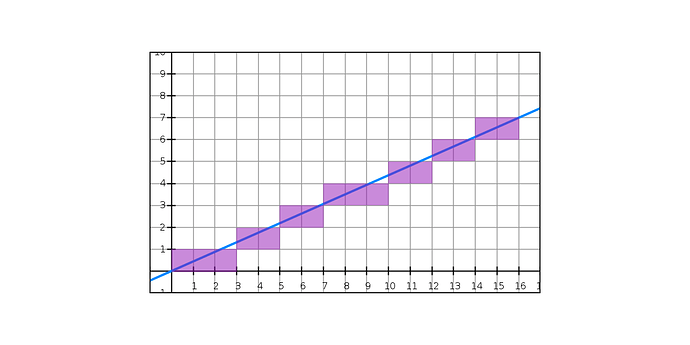
Basically, with the Bressenham line drawing approach we can imagine the (n,k) Euclidean pair as n / k, the slope of a line, and you can take the floor of the y value at each new integer x value and check if it is the same as for the previous x value. Kind of like this:
The author uses the term âquantizingâ to describe what is going on with the euclidean patterns, and I think this approach captures that really intuitively.
So, the cool thing about all of this is that in writing Tidal code, whenever we apply one pattern to another, we implicitly generate Euclidean stepping patterns, noticeable when the patterns divide up the cycle differently. Even if youâve never done this on purpose, youâve probably done this often.
For example:
d1 $ s âsupervibe*8â # n (run 3)
The n values for each sound will be 0 0 0 1 1 1 2 2 - the n values group together as 3,3,2.
Or for
d1 $ s âsupervibe*16â # n (run 7)
itâs 0 0 0 1 1 2 2 3 3 3 4 4 5 5 6 6, i.e., groups of 3 2 2 3 2 2 2
drawLine $ "x(7,16)" gives the pattern: |x--x-x-x--x-x-x-|
which uses the same groupings.
6 Likes
That's just beautiful, thanks for sharing!
This "most even distribution" (of events in discrete time) can be specified as "for each number w, and any two intervals of length w, the numbers of events in these intervals differ by at most one".
E.g., for x(7,16), x--x-x-x--x-x-x- , take w = 4, then intervals are x--x, --x-, -x-x, etc. (and it wraps around), always containing 1 or 2 xs.
I always wanted a two (or more) dimensional version of that: One dimension = time, other = instrument/note, perhaps.
The obvious generalization (for any w,h, consider number of events in w-by-h rectangles) is not too interesting, e.g.,
[0,0,1,0,0]
[1,0,0,0,0]
[0,0,0,1,0]
[0,1,0,0,0]
[0,0,0,0,1]
(e.g., each 2-by-3 rectangle contains 1 or 2 events) - and it only works for some choices of parameters
(e.g., sides of full rectangle must have gcd > 1)
and then, only few total numbers of events are realizable.
And if they are, it looks rather boring (it's cyclic shifts - for the cases that my program found)
[0,1,0,0,0,0,1,0,0,0]
[0,0,0,1,0,0,0,0,1,0]
[1,0,0,0,0,1,0,0,0,0]
[0,0,1,0,0,0,0,1,0,0]
[0,0,0,0,1,0,0,0,0,1]
I wonder if there is a way to relax the restrictions slightly, so that it works for any choice of parameters but is not arbitrary...
2 Likes
Just stumbled across this on the Tidal forums. Thanks for linking my blog post, Alex!
2 Likes
Interesting document on Euclidean rhythms, including references to actual pieces.
1 Like